Online Complex Number Calculator: Easy Operations in Polar and Rectangular Form

Are you struggling with complex number calculations for your math homework, engineering projects, or electrical circuit analysis? Look no further! Our free complex number calculator makes it simple to perform operations like addition, subtraction, multiplication, division, exponentiation, and even parallel impedance calculations. Whether you’re converting between rectangular and polar forms or handling advanced computations, this tool is designed for students, engineers, and math enthusiasts alike.

In this comprehensive guide, we’ll explore what complex numbers are, why a dedicated calculator is essential, and how you can use this tool yourself. Let’s dive in and simplify those imaginary numbers!

What Are Complex Numbers?

A visual representation of a complex number in both rectangular (x + yi) and polar (r ∠ θ) forms, showing the magnitude r and argument θ.

Complex numbers extend the real number system to include solutions to equations like $x^2 + 1 = 0$ , where no real number satisfies the condition. A complex number is typically expressed as $z = a + bi$ , where ‘a’ is the real part, ‘b’ is the imaginary part, and ‘i’ is the imaginary unit ( $\sqrt{-1}$ ).

These numbers can also be represented in polar form as $Z = r \big( \cos(\theta) + j \sin(\theta) \big)$ , where r is the magnitude (modulus) and θ is the argument (angle in degrees or radians). This dual representation is crucial for operations in fields like electrical engineering, signal processing, and quantum mechanics.

For instance, converting from rectangular to polar involves calculating $r = \sqrt{a^2 + b^2}$ and $\theta = \arctan\left(\frac{b}{a}\right)= \tan^{-1}\left(\frac{b}{a}\right)$ . Our calculator handles this conversion automatically, displaying results in both formats for clarity.

Key Operations on Complex Numbers

Working with complex numbers involves specific rules for basic operations:

Addition and Subtraction: Add or subtract the real and imaginary parts separately. For $Z_1 = a + iyb$ and $Z_2 = c + id$ , $Z_1+Z_2 = (a + c) + i(b + d)$ .
Multiplication: Use the distributive property: $z_1 \cdot z_2 = (ac - bd) + (ad + bc)i$ . In polar form, it’s simpler—multiply magnitudes and add angles.
Division: Multiply numerator and denominator by the conjugate of the denominator. Polar form: divide magnitudes and subtract angles.
Exponentiation: For $z^n$ , use De Moivre’s theorem in polar form: $[r \angle \theta]^n = r^n \angle (n\theta)$ .
Parallel (for Impedances): Common in electronics, $z_1 \parallel z_2 = \frac{z_1 \cdot z_2}{z_1 + z_2}$ .

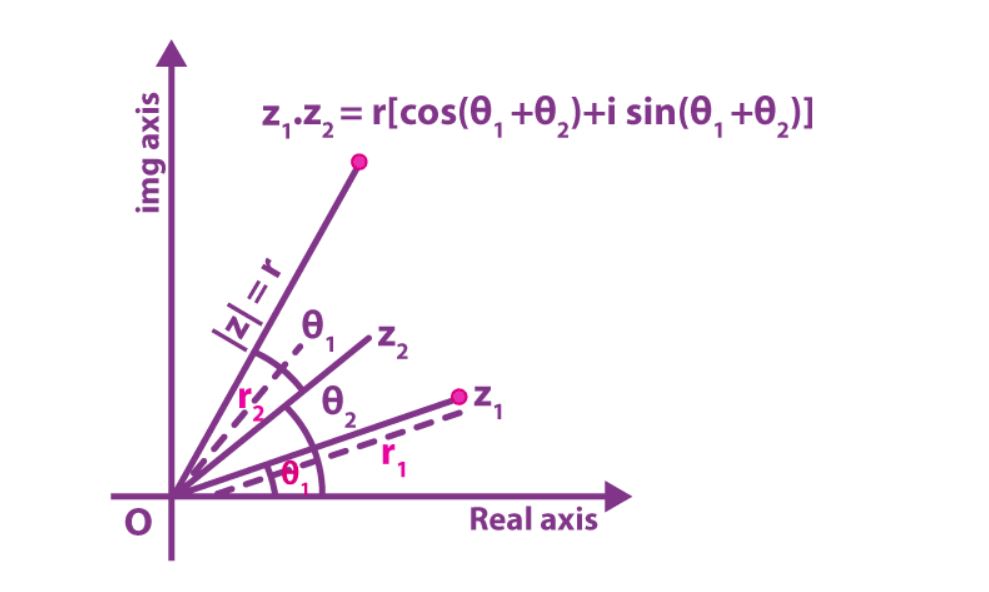
Diagram illustrating the multiplication of two complex numbers in polar form, where magnitudes multiply and angles add.

These operations can get tedious by hand, especially with large numbers or multiple steps. That’s where an online complex number calculator shines, saving time and reducing errors.

Why Choose This Free Complex Number Calculator?

Unlike some online tools that require subscriptions or have limited features, our calculator is completely free, open-source, and runs directly in your browser. Here’s what sets it apart:

Dual Display: Instantly see results in both rectangular (Re + Im i) and polar (magnitude ∠ angle°) forms.
Degree Mode (DEG): Angles are shown in degrees, perfect for engineering applications.
Comprehensive Operations: Supports +, -, ×, ÷, ^ (power), and || (parallel).
Real-Time Updates: As you input real and imaginary parts for $Z_1$ or $Z_2$ , the polar form updates automatically.

This tool is ideal for anyone searching for a “complex number calculator online” or “polar to rectangular converter free.” It’s lightweight, accurate, and handles edge cases like division by zero gracefully.

Benefits for Students and Professionals

Whether you’re a high school student learning about the complex plane or an electrical engineer calculating phasors, this tool streamlines your workflow. It eliminates manual calculations, which can be error-prone, especially for powers or divisions.

Compared to popular alternatives like Symbolab or Mathway, our version is offline-capable and fully customizable—no sign-ups required.

If you’re into electronics, the parallel operation (Z1 || Z2) is a bonus for combining impedances in circuits.

Complex Number Calculator

Z1:

Re(Z1):
Im(Z1):

0 ∠ 0° ↑↓

Z2:

Re(Z2):
Im(Z2):

0 ∠ 0° ↑↓

Answer

Conclusion

This free complex number calculator is a powerful, user-friendly tool for anyone dealing with imaginary numbers. By providing both rectangular and polar outputs, it bridges the gap between theory and practice.

If you have suggestions for improvements or need help customizing it, feel free to comment below. Happy calculating!