Directional Earth Fault Protection (67N) Explained for Impedance-Grounded Networks

This article focuses specifically on directional earth fault protection (ANSI 67N) for electrical networks with an impedance-grounded neutral. We’ll be releasing more articles soon that explore how directional earth protection behaves in other grounding systems. The goal is to give you a complete, system-by-system view of how earth fault protection works. Stay tuned—there’s much more coming.

In this article, we’ll walk through the function step by step:

Let’s break it all down.

What Is Directional Earth Fault Protection (67N)?

directional earth fault protection—designated ANSI 67N—is a protection method used to detect and locate earth faults in electrical networks. In networks with impedance grounding, capacitive currents and fault currents can look very similar. Directional earth fault protection helps tell them apart and ensures that only the faulty feeder gets disconnected.

When Does Directional Earth Fault Protection (67N) Operate?

Directional earth fault protection trips when two conditions are sustained for a preset time delay:

1. The residual current exceeds a chosen threshold, and
2. The phase angle between residual current and residual voltage falls inside the tripping zone.

The tripping zone is defined by a characteristic angle, \theta_{\text{rsd}}​.
Think of it as:

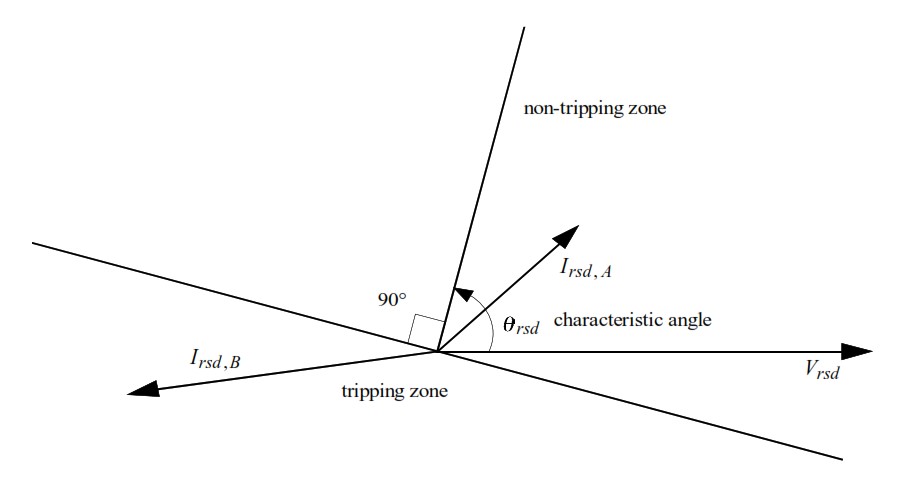
• A line perpendicular to the boundary between tripping and blocking zones
• Measured with respect to the polarizing voltage
• And the polarizing voltage is the residual voltage, V_{\text{rsd}}

Depending on where the residual current lies—in the tripping half-plane or the blocking half-plane—the protection either trips or stays silent.

The Two Half-Planes of Directional Earth Fault Protection

If the residual current vector falls inside the tripping zone (I_{\text{rsd,B}}​), the relay issues a trip. If it lands outside, in the blocking zone (I_{\text{rsd,A}}​), the relay does nothing.

Understanding these zones requires knowing how residual voltage and residual current are produced and measured. Let’s walk through each.

How Do You Measure Residual Voltage?

Residual voltage is the vector sum of the three phase-to-earth voltages:

• V_{\text{rsd}} = 3V_0 = V_1 + V_2 + V_3​

Two measurement methods exist:

1. Calculated Residual Voltage

The relay simply sums the three phase-to-earth voltages internally.

2. Measured Residual Voltage (Open-Delta VT)

This uses a voltage transformer with:

• Three secondary windings (one per phase)
• A tertiary winding connected in open delta

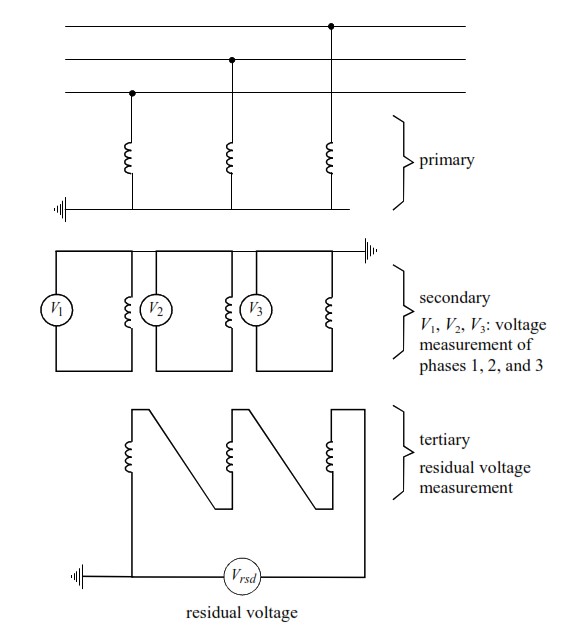
The open-delta output naturally produces the residual voltage—no calculation needed.

This is often more accurate, especially during distortion or transient events.

How Do You Measure Residual Current?

Residual current is also a vector sum:

• I_{\text{rsd}} = 3I_0 = I_1 + I_2 + I_3

It can be supplied to the relay in two ways:

1. Zero-Sequence CT (Toroidal CT Around the Feeder Cable)

Captures the true residual current directly.

2. Summed Phase CTs

The relay sums the secondary currents of the three phase CTs.

The sensitivity of earth fault protection depends on which method is used and how it is wired.

Residual Voltage During a Phase-to-Earth Fault

In a system grounded through a fault-limiting resistor, the residual voltage during a phase-to-earth fault can be calculated easily.

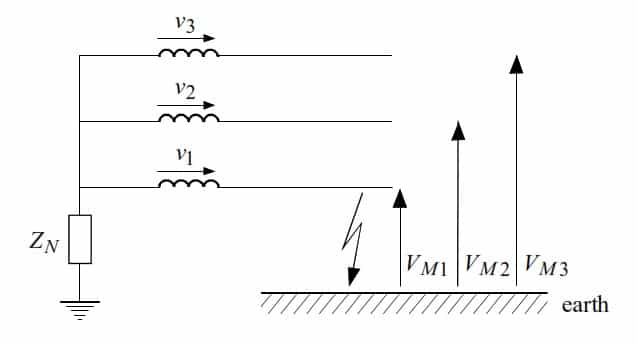
Let the measured phase-to-earth voltages be:

• V_{M1}​
• V_{M2}​
• V_{M3}

If phase 1 is faulted:

• V_{M1} = 0
• V_{M2} = V_2 - V_1
• V_{M3} = V_3 - V_1

The residual voltage becomes:

• V_{\text{rsd}} = V_{M1} + V_{M2} + V_{M3}​

Substituting values:

• V_{\text{rsd}} = 0 + (V_2 - V_1) + (V_3 - V_1)

• V_{\text{rsd}} = V_2 + V_3 - 2V_1

Given that:

• V_1 + V_2 + V_3 = 0

We get:

• V_{\text{rsd}} = -3V_1

For a fault on any phase q:

• |V_{\text{rsd}}| = 3V_n

Meaning the magnitude is three times the phase-to-neutral voltage.

How Do You Use Directional Earth Fault Protection (67N)?

67N is used to:

• Determine the direction of an earth fault
• Distinguish real fault current from capacitive current

This is especially important in impedance-grounded networks, where the natural capacitive current from long cables can be significant.

Sometimes the relay’s polarization is improved by measuring the neutral grounding resistor current:

• I_{\text{neut}} = -\frac{V_n}{R_n}

and since:

• V_{\text{rsd}} = -3V_n

The neutral current can also be expressed as:

• I_{\text{neut}} = \frac{V_{\text{rsd}}}{3R_n}

This additional measurement helps the relay distinguish capacitive currents from real earth faults.

How Does 67N Tell Fault Current From Capacitive Current?

Consider a network with several feeders. The total earth fault current is:

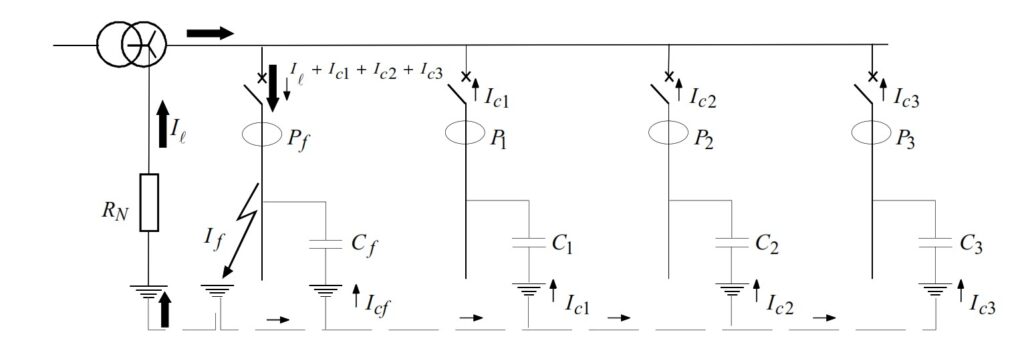
• I_f = I_l + I_{Cf} + I_{C1} + I_{C2} + I_{C3}

Where:

• I_l = \frac{V_n}{R_n} is the resistive current through the grounding resistor
• I_{Ci}​ are the individual capacitive currents of each feeder

The key point:

• Healthy feeders carry only capacitive current
• The faulty feeder carries both resistive current and capacitive currents

Directional earth fault protection uses phase angle differences between I_{\text{rsd}} and V_{\text{rsd}} to distinguish these two cases.

Tripping Zone vs. Blocking Zone

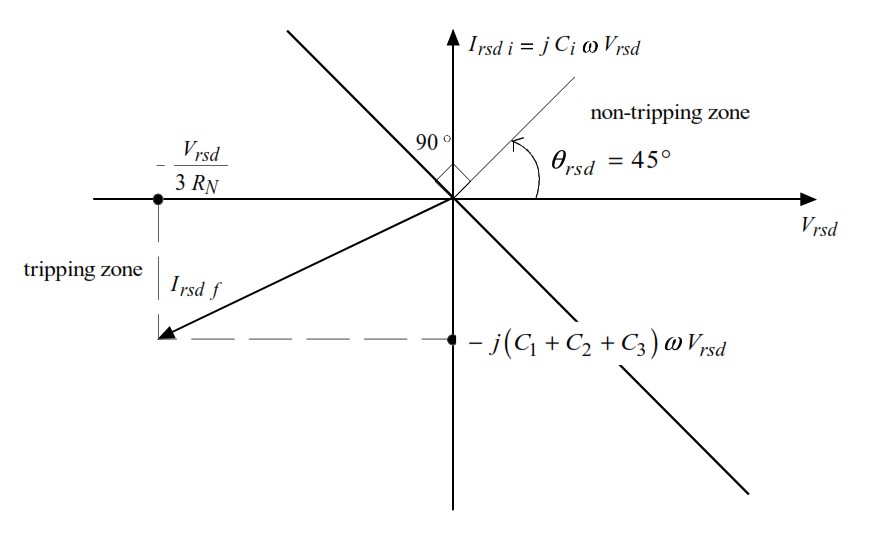
For the faulty feeder, the residual current is:

• I_{\text{rsd,f}} = \frac{V_n}{R_n} + 3j(C_1 + C_2 + C_3)\omega V_n

or rewritten using residual voltage:

• I_{\text{rsd,f}} = -\frac{V_{\text{rsd}}}{3R_n} - j(C_1 + C_2 + C_3)\omega V_{\text{rsd}}

For a healthy feeder:

• I_{\text{rsd,i}} = -I_{Ci}

• I_{\text{rsd,i}} = j C_i \omega V_{\text{rsd}}

This creates clear differences in the phase angle between voltage and current.

Because of these patterns:

Common Setting:

\theta_{\text{rsd}} = 45^\circ

The threshold current is set:

• Low enough to detect the faulty feeder
• High enough to avoid tripping on capacitive current alone

This is the key to reliable directional earth fault protection in impedance-grounded systems.

Conclusion

Directional earth fault protection (67N) is a powerful tool for safely and accurately detecting earth faults in impedance-grounded networks. It works by analyzing:

• Residual voltage
• Residual current
• Their phase relationship
• The characteristic angle that defines the tripping zone

By correctly setting these elements, protection engineers can ensure:

✔ Selective tripping
✔ Reliable fault detection
✔ Immunity to capacitive currents
✔ High network stability