L’algèbre vectorielle constitue un outil fondamental en ingénierie électrique, notamment dans l’analyse des circuits et des systèmes de protection. Elle permet de représenter des grandeurs physiques, telles que le courant ou la tension, non seulement par leur magnitude, mais également par leur direction.
Cet article met en lumière l’importance de la représentation vectorielle pour simplifier les calculs impliquant des quantités complexes, tout en offrant une compréhension plus claire et pratique de leur application.
Contenu de l'Article
Définition d’un Vecteur
Un vecteur représente une quantité dotée à la fois d’une magnitude (ou module) et d’une direction. Par exemple, imaginons un vecteur OP avec une magnitude ∣Z∣ formant un angle \theta par rapport à un axe de référence OX. Ce vecteur peut être décomposé en deux composantes orthogonales : une composante horizontale x et une composante verticale y.
Graphiquement, cela se représente sur un plan cartésien où :
- Le module ∣Z∣ est la longueur du vecteur.
- L’angle \theta est l’argument, noté argZ.
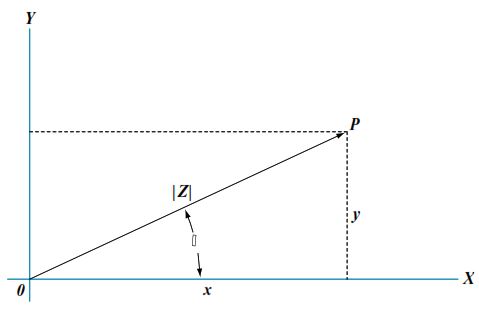
La notation conventionnelle pour exprimer un vecteur Z est ∣Z∣∠\theta, ce qui spécifie complètement sa représentation graphique ou sa conversion vers d’autres formes.
Représentation Algébrique
Pour utiliser les vecteurs dans des calculs, il est nécessaire de les exprimer algébriquement. Le vecteur Z, résultant de l’addition vectorielle de ses composantes x et y, s’écrit :
Z = x + jyIci, l’opérateur j indique que la composante y est perpendiculaire à x (rotation de 90° dans le sens anti-horaire). En nomenclature électrique :
- L’axe OX est l’axe « réel » ou « en phase ».
- L’axe OY est l’axe « imaginaire » ou « en quadrature ».
L’opérateur j vérifie les propriétés algébriques : j^2=−1.
Cette forme x+jy est appelée quantité complexe, représentant le vecteur en coordonnées rectangulaires.
À partir de cela, on déduit :
|Z| = \sqrt{x^2 + y^2}Et :
\theta = \arctan\left(\frac{y}{x}\right)= \tan^{-1}\left(\frac{y}{x}\right)Avec :
- x = |Z| \cos(\theta)
- y = |Z| \sin(\theta)
Formes Trigonométrique et Exponentielle
Le vecteur peut aussi s’exprimer de manière trigonométrique :
Z = |Z| \big( \cos(\theta) + j \sin(\theta) \big)En utilisant les identités d’Euler :
- \cos(\theta) = \frac{e^{j\theta} + e^{-j\theta}}{2}
- \sin(\theta) = \frac{e^{j\theta} - e^{-j\theta}}{2j}
On obtient la forme exponentielle :
Z = |Z| e^{j\theta}Ces formes facilitent les manipulations, surtout pour les quantités variables dans le temps, comme dans les circuits alternatifs.
Opérations sur les Nombres Complexes
Les nombres complexes peuvent être manipulés algébriquement ou sous forme polaire/exponentielle. Voici les principales opérations :
Addition et soustraction
Pour deux nombres complexes Z_1 = x_1 + jy_1 et Z_2 = x_2 + jy_2 :
- Z_1 + Z_2 = (x_1 + x_2) + j(y_1 + y_2)
- Z_1 - Z_2 = (x_1 - x_2) + j(y_1 - y_2)
On additionne ou soustrait composante par composante (réelle avec réelle, imaginaire avec imaginaire).
Multiplication
- Forme algébrique :
Z_1 \cdot Z_2 = (x_1 + jy_1)(x_2 + jy_2) = (x_1 x_2 - y_1 y_2) + j(x_1 y_2 + x_2 y_1) - Forme polaire/exponentielle :
Si Z_1 = |Z_1| e^{j\theta_1} et Z_2 = |Z_2| e^{j\theta_2}, alors :
Z_1 \cdot Z_2 = |Z_1||Z_2| e^{j(\theta_1 + \theta_2)}
En forme polaire, on multiplie les modules et on additionne les arguments.
Division
- Forme algébrique :
\frac{Z_1}{Z_2} = \frac{x_1 + jy_1}{x_2 + jy_2} = \frac{(x_1 + jy_1)(x_2 - jy_2)}{x_2^2 + y_2^2} = \frac{x_1 x_2 + y_1 y_2}{x_2^2 + y_2^2} + j \frac{y_1 x_2 - x_1 y_2}{x_2^2 + y_2^2} - Forme polaire/exponentielle :
\frac{Z_1}{Z_2} = \frac{|Z_1|}{|Z_2|} e^{j(\theta_1 - \theta_2)}
En forme polaire, on divise les modules et on soustrait les arguments.
Applications en Électricité
Calcul de la composante zéro V_0
Dans un système triphasé, la composante zéro V_0 représente la partie commune des tensions de phase, utile pour analyser les déséquilibres ou les défauts à la terre.
Pour un système triphasé avec les tensions V_a, V_b et V_c, la composante zéro se calcule par :
V_0 = \frac{V_a + V_b + V_c}{3}- V_a,V_b,V_c : tensions de chaque phase, exprimées sous forme complexe si l’angle de phase est pris en compte.
- V_0 : composante zéro.
Supposons un système triphasé symétrique avec :
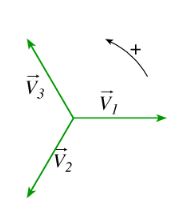
- V_a = 230 \angle 0^\circ = 230 e^{j 0}
- V_b = 230 \angle -120^\circ = 230 e^{-j 120^\circ}
- V_c = 230 \angle 120^\circ = 230 e^{j 120^\circ}
En développant avec Euler (e^{j\theta}=\cos\theta + j\sin\theta) :
V_a + V_b + V_c = V\Big(\cos 0 + j\sin 0\Big) + V\Big(\cos(-120^\circ) + j\sin(-120^\circ)\Big) + V\Big(\cos 120^\circ + j\sin 120^\circ\Big) = V\Big(1 + \cos 120^\circ + \cos 120^\circ\Big) + jV\Big(0 + \sin(-120^\circ) + \sin(120^\circ)\Big)Avec :
\cos 120^\circ = -\tfrac{1}{2}, \sin 120^\circ = +\tfrac{\sqrt{3}}{2}, \sin(-120^\circ)=-\tfrac{\sqrt{3}}{2}
Donc :
V_a + V_b + V_c = V\big(1 - \tfrac{1}{2} - \tfrac{1}{2}\big) + jV\big(0 - \tfrac{\sqrt{3}}{2} + \tfrac{\sqrt{3}}{2}\big) = 0 \;\;\Rightarrow\;\; V_0 = 0.
La composante zéro s’obtient en appliquant la formule :
V_0 = \frac{V_a + V_b + V_c}{3} = \frac{0}{3} = 0Dans ce cas, un système parfaitement équilibré a une composante zéro nulle.
En présence d’un déséquilibre ou d’un défaut à la terre,V_0 sera différent de zéro, ce qui permet de détecter et d’analyser ces situations.
Conclusion
L’algèbre vectorielle, telle que décrite dans cet article, transforme des concepts abstraits en outils pratiques pour l’analyse électrique. Elle relie les formes rectangulaires, polaires, trigonométriques et exponentielles, offrant une flexibilité pour les calculs complexes.
Pour les ingénieurs en protection de réseaux, maîtriser ces notions est indispensable pour limiter les effets des disturbances et assurer la stabilité des systèmes électriques.
